안녕하세요, 주말에 이미테이션 게임 영화를 너무 재미있게 보았습니다. 보다 보니 잠깐 공부했던 암호학 분야가 떠오르기도 했고… 튜링 선생님을 생각하면서 포스팅을 한번 작성해보도록 하겠습니다. 가벼운 마음으로 읽고 이해할 수 있을 정도의 내용을 다루려고 하며 크게 고전암호, 현대암호, 양자내성암호 세 파트로 나누어 포스팅을 작성해보겠습니다.
컴퓨터가 등장하기 이전에는 비트라는 개념이 존재하지 않았습니다. 암호학에서는 암호화되기 이전의 문서를 plaintext, 암호화된 이후의 문서를 ciphertext라고 하는데, plaintext와 ciphertext 모두 우리가 흔히 볼 수 있는 알파벳 혹은 숫자 등의 조합으로 이루어져 있었죠. 예전에는 어떠한 방식으로 ciphertext를 만들었을까요?
Substitution Cipher
Additive Cipher
말 그대로 하나의 문자를 다른 문자로 치환하는 형태의 암호입니다. plaintext가 “hello”, ciphertext가 “khoor”라면 ‘h’ → ‘k’, ‘e’ → ‘h’, ‘l’ → ‘o’, ‘o’ → ‘r’로 단순히 알파벳을 다른 알파벳으로 치환한 형태가 됩니다. 조금 더 체계를 갖춘 형태로 additive cipher가 있는데, 아래 표를 한번 봐보죠.
암호화에 사용할 key값은 plaintext의 각 알파벳을 얼마만큼 오른쪽에 위치한 알파벳으로 치환 할지에 따라 결정됩니다. 예시로 “DSDN”을 key=3으로 암호화한다고 해봅시다.
D를 3만큼 오른쪽으로 이동한 것이 ‘G’, N을 3만큼 오른쪽으로 이동시킨 것이 ‘Q’, ‘S’를 오른쪽으로 3만큼 이동시킨 것이 ‘V’가 되므로 plaintext “DSDN”을 key=3으로 암호화 했을 때의 ciphertext는 “GVGQ”가 될 것 입니다. 수신자가 ciphertext를 복호화 하기 위해서는 반대로 3만큼 왼쪽에 있는 알파벳으로 치환하면 됩니다. 송신자와 수신자가 key 값을 공유하고 있다면 손쉽게 암복호화할 수 있는 형태죠. 이러한 암호화 방식을 shift cipher 혹은 Caesar cipher라고도 하는데, 실제로 로마의 황제 카이사르가 사용했다고 합니다.
Multiplicative Cipher
더하는 것 말고 곱하는 방식도 있습니다. 이를 multiplicative cipher라 하는데 알파벳을 0부터 시작하여 커지는 정수에 대응 시켰을때 0 ~ 25의 값을 지니는 것을 알 수 있습니다. 해당 범위 내에서 곱셈의 역원을 갖는 정수 집합 Z_26에서 암복호화를 수행할 수 있습니다. 갑자기 정수 얘기가 나오니 머리가 조금 아픈 것 같지만, 간단하게 생각해서 암호화할 어떤 문자를 x, key 값을 k라고 했을때, x * k mod 26 = y가 암호화 과정이 되고, y * k^-1 mod 26 = x가 복호화 과정이 됩니다. 역시 제가 적어 놓고도 어려워 보이는데, 간단하게 예시를 통해 알아보겠습니다.
“hello”를 key=7로, multiplicative cipher로 암호화해보겠습니다. 우선 아까 봤던 표를 다시 한번 보겠습니다.
‘h’는 숫자 07에, ‘e’는 숫자 04에, ‘l’은 숫자 11에, ‘o’는 숫자 14에 대응되는 것을 확인할 수 있습니다. 각각에 대해 곱하기 7 모듈러 26 연산을 수행해보겠습니다.
‘h’ * 7 → 7 * 7 mod 26 = 23 → ‘x’
‘e’ * 7 → 4 * 7 mod 26 = 02 → ‘c’
‘l’ * 7 → 11 * 7 mod 26 = 25 → ‘z’
‘l’ * 7 → 11 * 7 mod 26 = 25 → ‘z’
‘o’ * 7 → 14 * 7 mod 26 = 20 → ‘u’
plaintext “hello”가 ciphertext “xczzu”로 암호화되었습니다. 그렇다면 복호화는 어떻게 할까요? 이때는 7의 26에 대한 곱셈의 역원(7 * x mod 26 = 1을 만족하는 x)인 15를 곱해주면 됩니다.
‘x’ * 15 → 23 * 15 mod 26 = 7 → ‘h’
‘c’ * 15 → 2 * 15 mod 26 = 4 → ‘e’
‘z’ * 15 → 25 * 15 mod 26 = 11 → ‘l’
‘z’ * 15 → 25 * 15 mod 26 = 11 → ‘l’
‘u’ * 15 → 20 * 15 mod 26 = 14 → ‘o’
additive cipher와는 다르게 multiplicative cipher는 모든 수에 대해 모듈러 26에 대한 곱셈의 역원이 존재하지는 않으므로 key 선정에 유의 해야 한다는 특징이 있습니다. 또 위 두 가지 방식을 혼합해 k1을 더하고 k2를 곱해서 암호화하고, k2^-1을 곱하고 k1을 빼서 복호화하는 형태의 affin cipher라는 것도 존재합니다.
Substitution cipher는 아래와 그림과 같이 이미테이션 게임에서 어린 앨런 튜링이 짝사랑하는 크리스토퍼에게 메시지를 전달할때도 나옵니다.
해당 이미지를 보면 substition cipher는 하나의 문자는 항상 같은 문자로 대응된다는 점을 알 수 있습니다. (’O’가 모두 ‘Q’로 대응되는 점)
Vigenre Cipher
아무리 고전 암호라지만 Substitution cipher는 너무 취약한 것 같습니다. 조금 더 복잡한 형태인 Vigenere Cipher에 대해 알아보겠습니다. Vigenere Cipher는 Vigenere라는 16세기 프랑스 수학자가 고안한 암호기법입니다. Plaintext, ciphertext ,key는 아래와 같은 관계를 갖습니다.
Plaintext: P1P2P3….
Ciphertxt: C1C2C3…
Key: [(k1, k2, …, km), (k1, k2, … km), …]
C1 = (P1 + K1) mod 26
P1 = (C1 - K1) mod 26
즉 Key가 길이 m인 문자열이 반복되는 형태로 이루어져 있습니다. 이러한 특징은 앞서 설명한 substitution cipher와는 다르게 하나의 문자가 서로 다른 문자로 대응될 수 있다는 장점이 있습니다. 예시로 “sheislistening”이라는 plaintext를 “pascal”이라는 key로 암호화해보겠습니다.
| Plaintext | s | h | e | i | s | l | i | s | t | e | n | i | n | g |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P(평문)의 정수값 | 18 | 07 | 04 | 08 | 18 | 11 | 08 | 18 | 19 | 04 | 13 | 08 | 13 | 06 |
| Key stream | 15 | 00 | 18 | 02 | 00 | 11 | 15 | 00 | 18 | 02 | 00 | 11 | 15 | 00 |
| C(암호문)의 정수값 | 07 | 07 | 22 | 10 | 18 | 22 | 23 | 18 | 11 | 6 | 13 | 19 | 02 | 06 |
| Ciphertext | H | H | W | K | S | W | X | S | L | G | N | T | C | G |
plaintext의 s가 각각 ‘H’, ‘S’ 등 다양하게 대응되는 것을 확인할 수 있습니다.
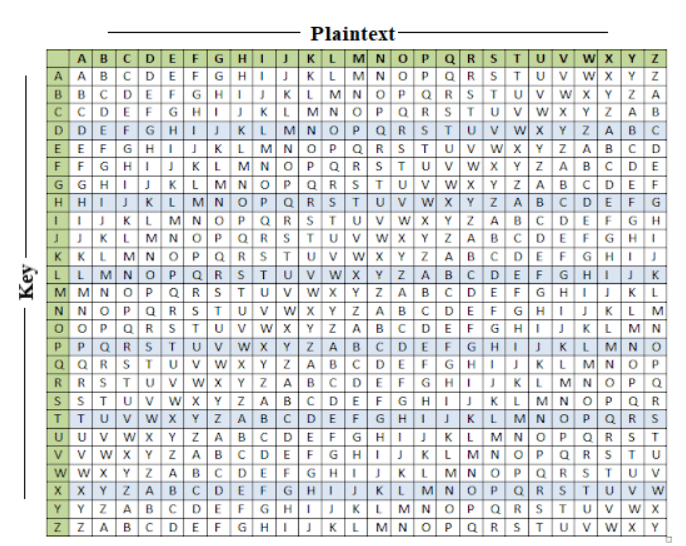
더하고 모듈러 연산을 수행하고 하는 것이 번거로우니, 아예 테이블을 참고해서 암복호화를 수행하기도 하는데요, 아래 그림은 Vigenere tableau라고 한답니다.
특정 plaintext를 key값만큼 미뤘을 때의 값을 plaintext와 key를 각각 열/행에 매칭시켜서 ciphertext를 찾아내는 방식이죠.
이 암호기법 역시 이미테이션 게임에서 나옵니다.
책이나 시집의 구절이 Key 값이 되고, 해당 문자열을 이용해 암/복호화를 수행하게 됩니다.
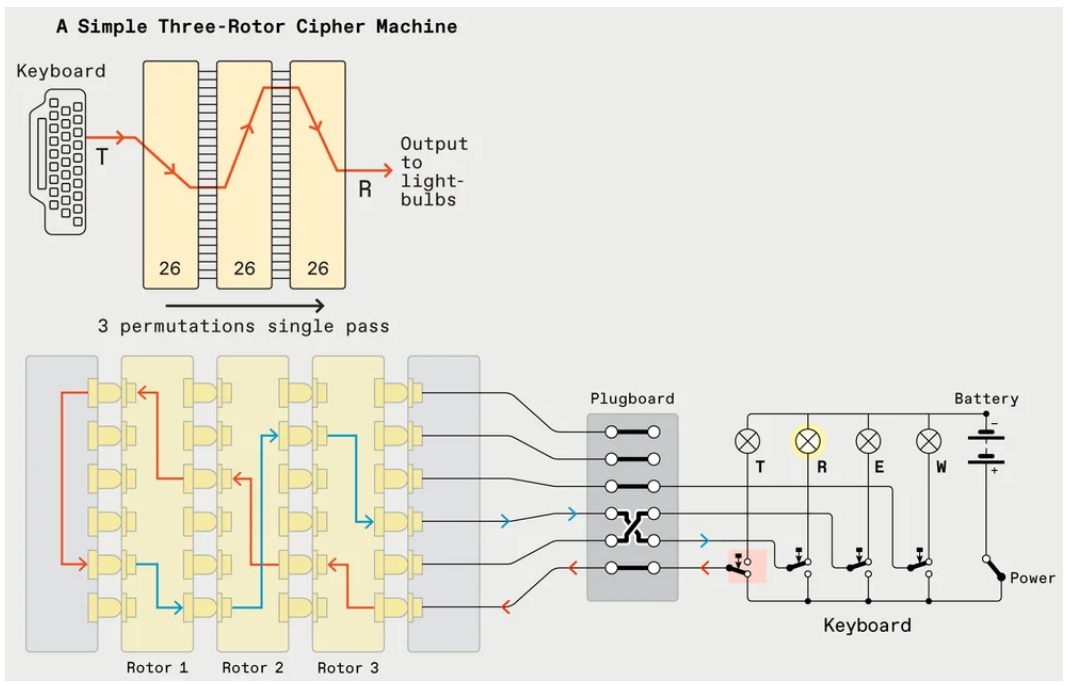
Rotor Cipher
Rotor Cipher는 위와 같이 내부의 rotor 장치에 미리 연결되어 있는 값을 통해 plaintext가 입력되었을 때, 대응되는 값을 ciphertext로 출력하는 형태의 암호기법입니다. 좀 더 응용시킨 형태가 이미테이션 게임에서 나오는 에니그마 머신인데, 매일 rotor 설정 값을 변경해 같은 plaintext를 입력값으로 주었을때 매일 전혀 다른 ciphertext가 출력 되도록 했다고 합니다.
Transposition Cipher
방금 전까지 치환을 했으니, 이번에는 섞어줄 차례입니다. 말 그대로 planintext의 순서를 바꾸는 형태의 암호 기법입니다. Plaintext를 어떻게 재배치할지 알려주는 인덱스를 설정함으로써 key 값을 설정합니다. 예시는 아래와 같습니다.
encryption key: [3, 1, 4, 5, 2] (plaintext의 3번째 문자가 1번째 자리에 옴 3→1, …)
decryption key: [2, 5, 1, 3, 4] (ciphertext의 2번째 문자가 1번째 자리에 옴 2→1, …)
를 갖고 “hello”라는 문자열을 암호화 해보겠습니다.
| i | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| plaintext[i] | ‘h’ | ‘e’ | ‘l’ | ‘l’ | ‘o’ |
| ciphertext[i] | ‘l’ | ‘h’ | ‘l’ | ‘o’ | ‘e’ |
plaintext “hello”가 ciphertext “lhloe”로 암호화되었습니다. 복호화는 decryption key를 갖고 재배치 작업을 수행하면 됩니다.
마무리
지금까지 고전 암호에 대해 간단하게 알아봤습니다. 간단한 암호 기법이지만 암호화 후의 ciphertext는 원래 어떤 의미를 지녔는지 파악하기 힘들어 보입니다. 하지만 컴퓨터가 있다면…? 이야기가 달라집니다. additive, multiplicative cipher의 경우 key 값 0 ~ 25에 대해 bruteforce 작업을 수행하면 금세 plaintext 복호화가 가능해질 겁니다. Vigenere 암호 기법 역시 Kasisiki test와 같은 방법을 이용한다면 취약할 수 있다는 것이 알려져 있습니다. Transposition cipher의 경우 key 값을 매우 크게 한다면 N! 만큼 bruteforce 해야 하기 때문에 안전하지 않을까 생각할 수 있지만, 저희가 간과한 매우 중요한 한 가지 부분이 있습니다.
“그 Key를 어떻게 전달할건데…?”
지금까지 살펴본 암호 기법들은 전부 동일한 key 를 통해 암복호화를 수행합니다. 이러한 암호 기법들을 대칭키 암호라 하는데, key를 전달하는 과정에서 누군가 엿 볼 수도 있고, 특히나 네트워크 환경에서는 mitm(man-in-the-middle attack)을 통해 key를 탈취할 위험성도 존재합니다.
현대 암호에서는 고전 암호의 취약점과 이러한 키 공유 문제를 nice하게 해결하는데, 다음 현대 암호 포스팅에서 다뤄보도록 하겠습니다.